شرح: كيف تقوم L1 Regularization بتحديد الميزات تلقائيًا؟

تحديد الميزات (Feature Selection) هو عملية اختيار مجموعة فرعية مثالية من الميزات من مجموعة معينة من الميزات؛ والمجموعة الفرعية المثالية هي تلك التي تزيد من أداء النموذج على المهمة المحددة.

يمكن أن يكون تحديد الميزات عملية يدوية أو بالأحرى صريحة عند إجرائها باستخدام طرق التصفية (filter methods) أو التغليف (wrapper methods). في هذه الطرق، تتم إضافة الميزات أو إزالتها بشكل متكرر بناءً على قيمة مقياس ثابت، والذي يحدد مدى أهمية الميزة في إجراء التنبؤ. يمكن أن تكون المقاييس هي كسب المعلومات، أو التباين، أو إحصائية مربع كاي، وستتخذ الخوارزمية قرارًا بقبول/رفض الميزة مع مراعاة حد ثابت على المقياس. تجدر الإشارة إلى أن هذه الطرق ليست جزءًا من مرحلة تدريب النموذج ويتم إجراؤها قبل ذلك.

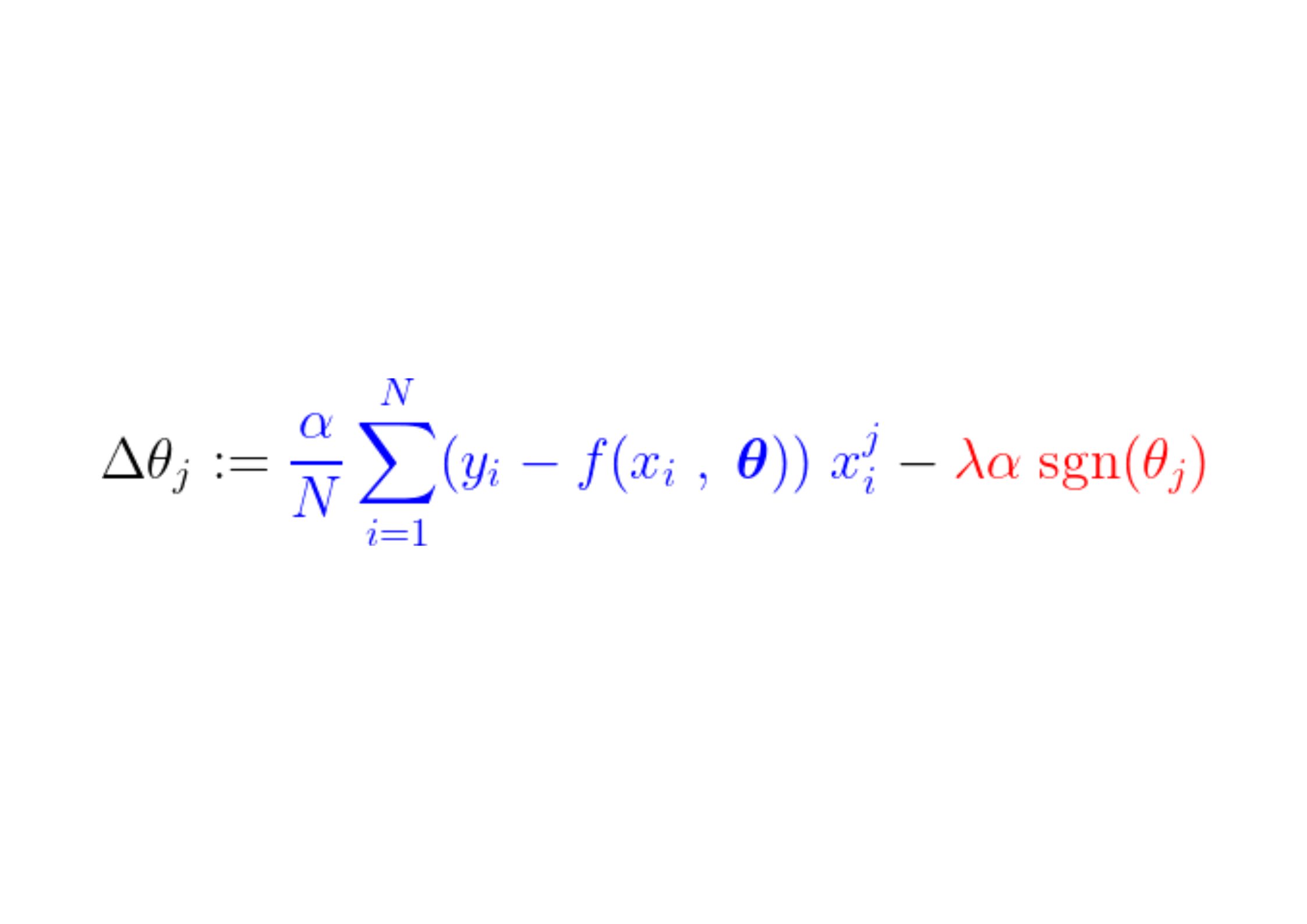
تقوم الطرق المضمنة (Embedded methods) بتحديد الميزات ضمنيًا، دون استخدام أي معايير اختيار محددة مسبقًا واستخلاصها من بيانات التدريب نفسها. تعد عملية تحديد الميزات الجوهرية هذه جزءًا من مرحلة تدريب النموذج. يتعلم النموذج تحديد الميزات وإجراء تنبؤات ذات صلة في نفس الوقت. في الأقسام اللاحقة، سنصف دور التنظيم (regularization) في إجراء عملية تحديد الميزات الجوهرية هذه، مع التركيز على تقنية L1 regularization ودورها في تحسين نماذج تعلم الآلة.

التسوية وتعقيد النموذج: استراتيجيات متقدمة لتحسين الأداء

التنظيم (Regularization) هو عملية معاقبة تعقيد النموذج لتجنب الزيادة في التوفيق (Overfitting) وتحقيق التعميم (Generalization) على المهمة.

هنا، تعقيد النموذج يماثل قدرته على التكيف مع الأنماط في بيانات التدريب. بافتراض نموذج متعدد الحدود بسيط في ‘x‘ بدرجة ‘d‘، كلما زادت الدرجة ‘d‘ لكثير الحدود، يحقق النموذج مرونة أكبر لالتقاط الأنماط في البيانات المرصودة. هذه المرونة الزائدة قد تؤدي إلى حفظ النموذج للبيانات التدريبية بدلاً من تعلم الأنماط الحقيقية، وهو ما يقلل من قدرته على التعميم على بيانات جديدة.

التحميل الزائد والتحميل الناقص (Overfitting and Underfitting)

عند محاولة ملاءمة نموذج متعدد الحدود بدرجة d = 2 على مجموعة من عينات التدريب المستمدة من متعدد حدود من الدرجة الثالثة مع بعض الضوضاء، لن يتمكن النموذج من التقاط توزيع العينات بدرجة كافية. يفتقر النموذج ببساطة إلى المرونة أو التعقيد اللازم لنمذجة البيانات الناتجة عن متعددات الحدود من الدرجة 3 (أو أعلى). يقال إن هذا النموذج يعاني من التحميل الناقص (under-fit) على بيانات التدريب. يشير التحميل الناقص إلى أن النموذج بسيط جدًا ولا يمكنه التقاط الأنماط الأساسية في البيانات.

بالعمل على نفس المثال، نفترض الآن أن لدينا نموذجًا بدرجة d = 6. الآن مع زيادة التعقيد، يجب أن يكون من السهل على النموذج تقدير متعدد الحدود التكعيبي الأصلي الذي تم استخدامه لإنشاء البيانات (مثل تعيين معاملات جميع المصطلحات ذات الأس > 3 إلى 0). إذا لم يتم إنهاء عملية التدريب في الوقت المناسب، فسيستمر النموذج في استخدام مرونته الإضافية لتقليل الخطأ بشكل أكبر والبدء في التقاط العينات الضوضائية أيضًا. سيؤدي ذلك إلى تقليل خطأ التدريب بشكل كبير، ولكن النموذج الآن يعاني من التحميل الزائد (overfits) على بيانات التدريب. ستتغير الضوضاء في إعدادات العالم الحقيقي (أو في مرحلة الاختبار) وأي معرفة تستند إلى التنبؤ بها ستتعطل، مما يؤدي إلى ارتفاع خطأ الاختبار. التحميل الزائد يعني أن النموذج معقد جدًا ويتعلم الضوضاء بدلاً من الإشارة الحقيقية.

كيفية تحديد التعقيد الأمثل للنموذج؟

في البيئات العملية، غالبًا ما يكون لدينا فهم محدود أو معدوم لعملية توليد البيانات أو التوزيع الحقيقي للبيانات. يعد إيجاد النموذج الأمثل بالتعقيد المناسب، بحيث لا يحدث نقص في التوفيق أو زيادة فيه، تحديًا كبيرًا. يتطلب ذلك استخدام طرق فعالة لتقييم أداء النماذج وتحديد التعقيد المناسب الذي يحقق أفضل توازن بين الدقة والعمومية. من خلال استخدام مقاييس تقييم مناسبة وتقنيات مثل التحقق المتقاطع، يمكن للمختصين تحديد النموذج الذي يعطي أفضل أداء على البيانات غير المرئية، وبالتالي تجنب مشاكل التوفيق الزائد أو الناقص.

إحدى التقنيات الممكنة هي البدء بنموذج قوي بما فيه الكفاية ثم تقليل تعقيده عن طريق اختيار الميزات. كلما قلت الميزات، قل تعقيد النموذج.

كما ناقشنا في القسم السابق، يمكن أن يكون اختيار الميزات صريحًا (طرق التصفية، طرق الالتفاف) أو ضمنيًا. يجب التخلص من الميزات الزائدة التي ليس لها أهمية كبيرة في تحديد قيمة المتغير المستهدف لتجنب تعلم النموذج لأنماط غير مترابطة فيها. التسوية (Regularization) تؤدي أيضًا مهمة مماثلة. إذن، كيف يرتبط التسوية (Regularization) واختيار الميزات لتحقيق هدف مشترك وهو تعقيد النموذج الأمثل؟ يعتبر تقليل التعقيد في نماذج تعلم الآلة أمرًا بالغ الأهمية لتحسين الأداء وتجنب التجاوز، وهو ما يركز عليه كل من التسوية واختيار الميزات.

تنظيم L1 كمحدد للميزات

بالاستمرار مع نموذجنا متعدد الحدود، نمثله كدالة f، مع مدخلات x، ومعاملات θ ودرجة d،

بالنسبة للنموذج متعدد الحدود، يمكن اعتبار كل قوة للإدخال x_i كميزة، لتشكيل متجه بالشكل التالي:

نحدد أيضًا دالة هدف، والتي يؤدي تقليلها إلى المعلمات المثالية θ* وتتضمن مصطلح regularization (التنظيم) الذي يعاقب تعقيد النموذج.

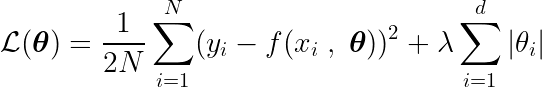
لتحديد الحد الأدنى لهذه الدالة، نحتاج إلى تحليل جميع النقاط الحرجة، أي النقاط التي يكون فيها الاشتقاق صفراً أو غير معرف.

يمكن كتابة المشتق الجزئي بالنسبة لإحدى المعلمات، θj، على النحو التالي:

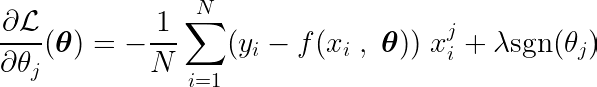
حيث يتم تعريف الدالة sgn على النحو التالي:

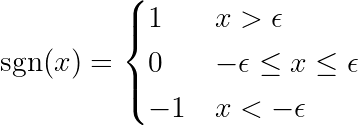
ملاحظة: مشتقة الدالة المطلقة تختلف عن دالة الإشارة (sgn) المعرفة أعلاه. المشتقة الأصلية غير معرفة عند x = 0. نقوم بتوسيع التعريف لإزالة نقطة الانعطاف عند x = 0 ولجعل الدالة قابلة للاشتقاق عبر نطاقها بأكمله. علاوة على ذلك، تستخدم أطر عمل تعلم الآلة (ML) هذه الدوال الموسعة عندما تتضمن العمليات الحسابية الأساسية الدالة المطلقة. تحقق من هذا الرابط في منتدى بايتورش (PyTorch).

عن طريق حساب المشتقة الجزئية لدالة الهدف بالنسبة لمعامل واحد θj، ومساواتها بالصفر، يمكننا بناء معادلة تربط القيمة المثلى لـ θj بالتنبؤات والأهداف والميزات.

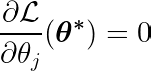
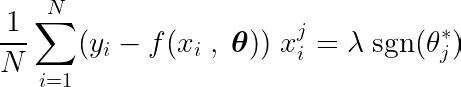
دعونا نفحص المعادلة أعلاه. إذا افترضنا أن المدخلات والأهداف كانت متمركزة حول المتوسط (أي أن البيانات قد تم توحيدها في خطوة المعالجة المسبقة)، فإن المصطلح الموجود على الجانب الأيسر (LHS) يمثل بشكل فعال التباين بين الميزة رقم j والفرق بين القيم المتوقعة والمستهدفة.

التباين الإحصائي بين متغيرين يحدد كمية تأثير أحد المتغيرات على قيمة المتغير الثاني (والعكس صحيح).

دالة الإشارة في الطرف الأيمن تجبر التباين في الطرف الأيسر على افتراض ثلاث قيم فقط (حيث أن دالة الإشارة تُرجع فقط ‎-1‎، 0 و 1). إذا كانت الميزة j غير ضرورية ولا تؤثر على التنبؤات، فسيكون التباين قريبًا من الصفر، مما يؤدي إلى جعل المعامل المقابل θj* صفرًا. ينتج عن هذا حذف الميزة من النموذج. هذه العملية تساعد في تقليل التعقيد وتحسين أداء النموذج.

تخيل دالة الإشارة كأخدود نحتته المياه. يمكنك السير في الأخدود (أي مجرى النهر)، ولكن للخروج منه، ستواجه حواجز ضخمة أو منحدرات شديدة. يعمل التنظيم L1 (L1 Regularization) على إحداث تأثير “عتبة” مماثل لتدرج دالة الخسارة. يجب أن يكون التدرج قويًا بما يكفي لكسر الحواجز أو أن يصبح صفرًا، مما يؤدي في النهاية إلى جعل قيمة المعامل صفرًا.

لتقديم مثال أكثر واقعية، ضع في اعتبارك مجموعة بيانات تحتوي على عينات مشتقة من خط مستقيم (معاملة بمعاملين) مع بعض الضوضاء المضافة. يجب ألا يحتوي النموذج الأمثل على أكثر من معاملين، وإلا فسوف يتكيف مع الضوضاء الموجودة في البيانات (مع الحرية/القوة المضافة لكثير الحدود). تغيير معاملات القوى الأعلى في نموذج كثير الحدود لا يؤثر على الفرق بين الأهداف وتوقعات النموذج، وبالتالي يقلل من تباينها مع الميزة.

أثناء عملية التدريب، تتم إضافة/طرح خطوة ثابتة من تدرج دالة الخسارة. إذا كان تدرج دالة الخسارة (MSE – متوسط مربع الخطأ) أصغر من الخطوة الثابتة، فسيصل المعامل في النهاية إلى قيمة 0. لاحظ المعادلة أدناه، التي تصور كيفية تحديث المعاملات باستخدام الانحدار التدريجي (Gradient Descent):

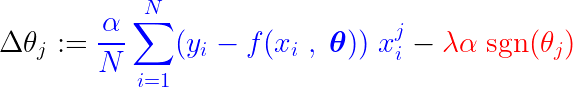
إذا كان الجزء الأزرق أعلاه أصغر من λα، وهو رقم صغير جدًا في حد ذاته، فإن Δθj هو تقريبًا خطوة ثابتة λα. تعتمد إشارة هذه الخطوة (الجزء الأحمر) على sgn(θj)، الذي يعتمد خرجه على θj. إذا كانت قيمة θj موجبة، أي أكبر من ε، فإن sgn(θj) تساوي 1، وبالتالي تجعل Δθj تقريبًا تساوي –λα، مما يدفعها نحو الصفر.

لكبح الخطوة الثابتة (الجزء الأحمر) التي تجعل المعامل صفرًا، يجب أن يكون تدرج دالة الخسارة (الجزء الأزرق) أكبر من حجم الخطوة. للحصول على تدرج أكبر لدالة الخسارة، يجب أن تؤثر قيمة الميزة على خرج النموذج بشكل كبير.

هذه هي الطريقة التي يتم بها التخلص من الميزة، أو بشكل أكثر دقة، المعامل المقابل لها، الذي لا ترتبط قيمته بخرج النموذج، يتم تصفيره بواسطة التنظيم L1 (L1 Regularization) أثناء التدريب.

قراءات إضافية وخلاصة

• للحصول على المزيد من الرؤى حول هذا الموضوع، قمت بنشر سؤال على ريديت r/MachineLearning، والمتابعة تحتوي على تفسيرات مختلفة قد ترغب في قراءتها.

• لدى ماديار أيتباييف أيضًا مدونة مثيرة للاهتمام تغطي نفس السؤال، ولكن مع شرح هندسي.

• مدونة برايان كينغ تشرح التنظيم من منظور احتمالي.

• هذا النقاش على موقع CrossValidated يشرح لماذا يشجع معيار L1 النماذج المتفرقة. مدونة مفصلة كتبها موكول رانجان تشرح لماذا يشجع معيار L1 المعاملات على أن تصبح صفرًا وليس معيار L2.

“L1 Regularization يقوم باختيار الميزات” هي عبارة بسيطة يتفق معها معظم متعلمي ML، دون الخوض في كيفية عملها داخليًا. هذه المدونة هي محاولة لتقديم فهمي ونموذجي الذهني للقراء من أجل الإجابة على السؤال بطريقة بديهية. للاقتراحات والشكوك، يمكنك العثور على بريدي الإلكتروني على موقعي الإلكتروني. استمر في التعلم واستمتع بيوم جميل!