عندما يلتقي علم الفيزياء بالتمويل: استخدام الذكاء الاصطناعي لحل معادلة بلاك-شولز

إخلاء مسؤولية: هذه ليست نصيحة مالية. أنا حاصل على درجة الدكتوراه في هندسة الطيران مع تركيز قوي على تعلم الآلة: أنا لست مستشارًا ماليًا. هذه المقالة مخصصة فقط لإظهار قوة الشبكات العصبية المستنيرة بالفيزياء (PINNs) في سياق مالي.

عندما كان عمري 16 عامًا، وقعت في حب الفيزياء. كان السبب بسيطًا ولكنه قوي: اعتقدت أن الفيزياء عادلة.

لم يحدث أبدًا أن أخطأت في تمرين لأن سرعة الضوء تغيرت بين عشية وضحاها، أو لأنه فجأة يمكن أن تكون e^x سالبة. في كل مرة قرأت فيها ورقة فيزيائية وفكرت، “هذا لا يبدو منطقيًا،” اتضح أن أنا من لم يكن يفهم.

إذًا، الفيزياء عادلة دائمًا، ولهذا السبب فهي دائمًا مثالية. وتعرض الفيزياء هذا الكمال والعدالة من خلال مجموعة القواعد الخاصة بها، والتي تُعرف باسم المعادلات التفاضلية.

أبسط معادلة تفاضلية أعرفها هي هذه:

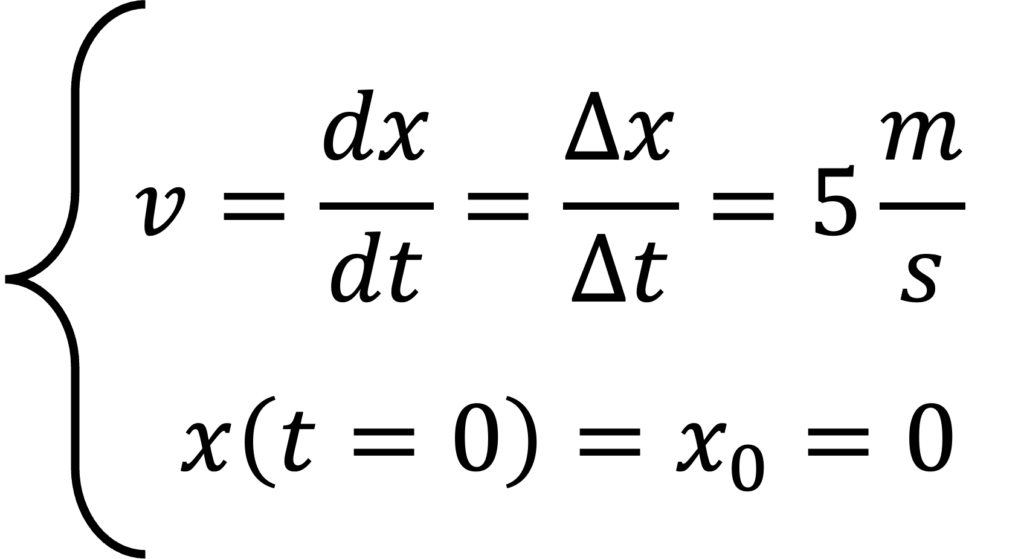
بسيط جدًا: نبدأ هنا، x₀=0، في الوقت t=0، ثم نتحرك بسرعة ثابتة قدرها 5 م/ث. هذا يعني أنه بعد ثانية واحدة، نكون على بعد 5 أمتار (أو أميال، إذا كنت تفضل ذلك) من الأصل؛ بعد ثانيتين، نكون على بعد 10 أمتار من الأصل؛ بعد 43128 ثانية… أعتقد أنك فهمت.

كما كنا نقول، هذا مكتوب على الحجر: مثالي، مثالي، ولا جدال فيه. ومع ذلك، تخيل هذا في الحياة الواقعية. تخيل أنك في نزهة أو تقود السيارة. حتى إذا بذلت قصارى جهدك للذهاب بسرعة مستهدفة، فلن تتمكن أبدًا من الحفاظ عليها ثابتة. سوف يتسارع ذهنك في أجزاء معينة؛ ربما ستصاب بالشرود الذهني، ربما ستتوقف عند الأضواء الحمراء، وعلى الأرجح مزيج مما سبق. لذلك ربما تكون المعادلة التفاضلية البسيطة التي ذكرناها سابقًا غير كافية. ما يمكننا فعله هو محاولة التنبؤ بموقعك من المعادلة التفاضلية، ولكن بمساعدة الذكاء الاصطناعي. هذا المفهوم بالغ الأهمية في نمذجة الأنظمة المعقدة.

يتم تطبيق هذه الفكرة في الشبكات العصبية المستنيرة بالفيزياء (PINN). سنصفها لاحقًا بالتفصيل، ولكن الفكرة هي أننا نحاول مطابقة كل من البيانات وما نعرفه من المعادلة التفاضلية التي تصف الظاهرة. هذا يعني أننا نفرض على حلنا أن يلبي بشكل عام ما نتوقعه من الفيزياء. أعلم أن هذا يبدو وكأنه سحر أسود، أعدك أنه سيكون أكثر وضوحًا خلال هذا المقال.

الآن، السؤال الكبير:

ما علاقة التمويل بالفيزياء والشبكات العصبية المستندة إلى الفيزياء؟

حسنًا، اتضح أن المعادلات التفاضلية ليست مفيدة فقط للمهتمين بقوانين الكون الطبيعي، بل يمكن أن تكون مفيدة أيضًا في النماذج المالية. على سبيل المثال، يستخدم نموذج Black-Scholes معادلة تفاضلية لتحديد سعر خيار الشراء، مع افتراضات صارمة معينة، للحصول على محفظة خالية من المخاطر.

الهدف من هذه المقدمة المعقدة للغاية كان ذا شقين:

• إرباكك قليلًا، حتى تستمر في القراءة 🙂
• إثارة فضولك بما يكفي لرؤية إلى أين يتجه كل هذا.

آمل أن أكون قد نجحت 😁. إذا فعلت ذلك، فستتبع بقية المقالة هذه الخطوات:

1. سوف نناقش نموذج Black-Scholes، وافتراضاته، ومعادلته التفاضلية
2. سوف نتحدث عن الشبكات العصبية المستندة إلى الفيزياء (PINNs)، ومن أين أتت، ولماذا هي مفيدة
3. سنقوم بتطوير الخوارزمية الخاصة بنا التي تدرب PINN على Black-Scholes باستخدام Python و Torch و OOP.
4. سنعرض نتائج الخوارزمية الخاصة بنا.

أنا متحمس! إلى المختبر! 🧪

1. نموذج بلاك سكولز: نظرة متعمقة

إذا كنت مهتمًا بالاطلاع على الورقة البحثية الأصلية لنموذج بلاك-شولز، يمكنك العثور عليها هنا. بالتأكيد تستحق القراءة 🙂

حسنًا، الآن يجب أن نفهم عالم التمويل الذي نحن فيه، وما هي المتغيرات، وما هي القوانين التي تحكمه. فهم أساسيات التمويل وعلاقتها بـ Black-Scholes أمر بالغ الأهمية.

أولاً، في مجال التمويل، توجد أداة قوية تسمى خيار الشراء (call option). يمنحك خيار الشراء الحق (وليس الالتزام) في شراء سهم بسعر معين في المستقبل المحدد (لنفترض بعد عام من الآن)، وهو ما يسمى بسعر التنفيذ (strike price).

الآن، دعونا نفكر في الأمر للحظة، أليس كذلك؟ لنفترض أن سعر السهم اليوم هو 100 دولار. لنفترض أيضًا أننا نمتلك خيار شراء بسعر تنفيذ 100 دولار. الآن، لنفترض أنه في غضون عام واحد، ارتفع سعر السهم إلى 150 دولارًا. هذا رائع! يمكننا استخدام خيار الشراء هذا لشراء السهم ثم إعادة بيعه على الفور! لقد حققنا للتو ربحًا قدره 150 دولارًا – 100 دولار = 50 دولارًا. من ناحية أخرى، إذا انخفض سعر السهم في غضون عام واحد إلى 80 دولارًا، فلا يمكننا فعل ذلك. في الواقع، من الأفضل لنا عدم ممارسة حقنا في الشراء على الإطلاق، حتى لا نخسر المال.

إذًا، بعد أن فكرنا في الأمر، فإن فكرة شراء سهم و بيع خيار تبدو متكاملة تمامًا. ما أعنيه هو أن عشوائية سعر السهم (حقيقة أنه يرتفع وينخفض) يمكن في الواقع تخفيفها من خلال الاحتفاظ بالعدد الصحيح من الخيارات. وهذا ما يسمى بالتحوط الدلتا (delta hedging). وهو استراتيجية أساسية في إدارة المخاطر.

بناءً على مجموعة من الافتراضات، يمكننا اشتقاق سعر الخيار العادل من أجل الحصول على محفظة خالية من المخاطر. هذا المفهوم جوهري لنموذج Black-Scholes.

لا أريد أن أملّك بكل تفاصيل الاشتقاق (بصراحة، ليس من الصعب متابعتها في الورقة الأصلية)، ولكن المعادلة التفاضلية للمحفظة الخالية من المخاطر هي هذه:

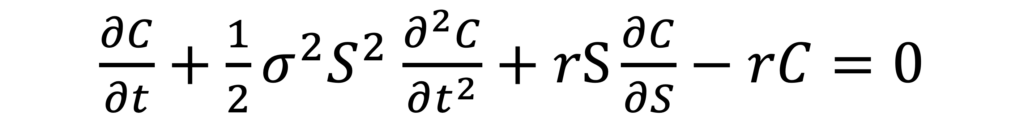
حيث:

• C هو سعر الخيار في الوقت t
• sigma هو تقلب السهم
• r هو المعدل الخالي من المخاطر
• t هو الوقت (مع t=0 الآن و T عند تاريخ الانتهاء)
• S هو سعر السهم الحالي

من هذه المعادلة، يمكننا اشتقاق السعر العادل لخيار الشراء للحصول على محفظة خالية من المخاطر. المعادلة مغلقة وتحليلية، وتبدو هكذا:

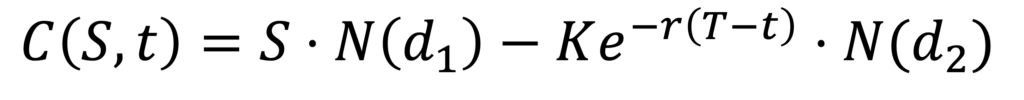
مع:

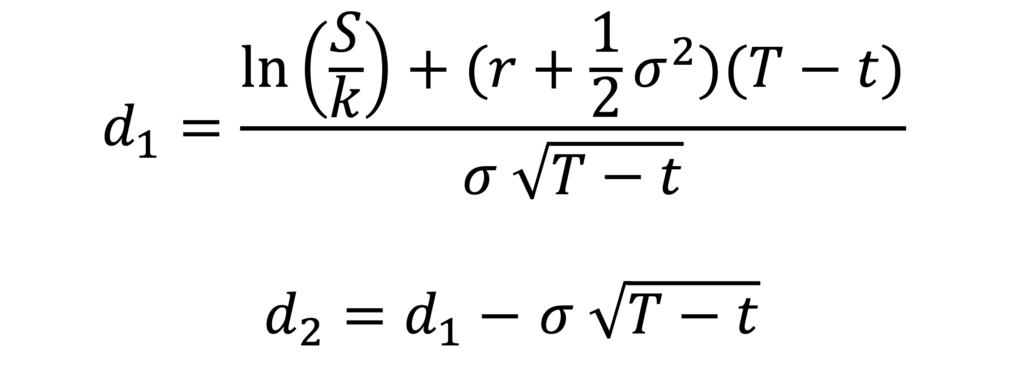
حيث N(x) هي دالة التوزيع التراكمي (CDF) للتوزيع الطبيعي القياسي، K هو سعر التنفيذ، و T هو تاريخ الانتهاء.

على سبيل المثال، هذا هو مخطط سعر السهم (x) مقابل خيار الشراء (y)، وفقًا لنموذج بلاك-شولز.

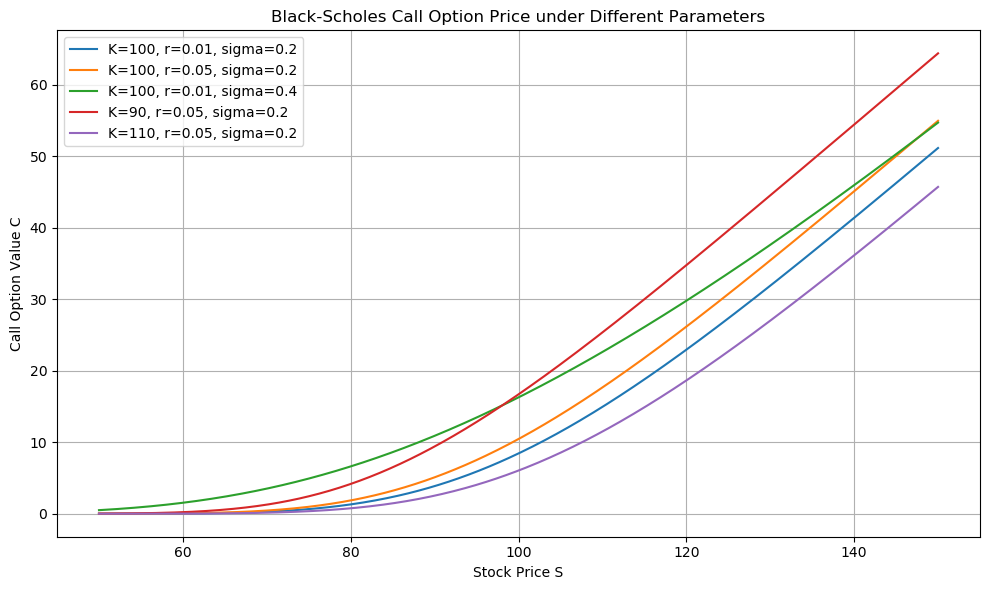
الآن هذا يبدو رائعًا وكل شيء، ولكن ما علاقة هذا بالفيزياء و PINN؟ يبدو أن المعادلة تحليلية، فلماذا PINN؟ لماذا الذكاء الاصطناعي؟ لماذا أقرأ هذا على الإطلاق؟ الجواب أدناه 👇:

2. الشبكات العصبية المُستنيرة بالفيزياء (Physics Informed Neural Networks)

إذا كنت مهتمًا بالشبكات العصبية المستنيرة بالفيزياء (Physics Informed Neural Networks – PINNs)، يمكنك الاطلاع على الورقة الأصلية هنا. مرة أخرى، تستحق القراءة. 🙂

الآن، المعادلة أعلاه تحليلية، ولكن مرة أخرى، هذه معادلة لسعر عادل في سيناريو مثالي. ماذا يحدث إذا تجاهلنا هذا للحظة وحاولنا تخمين سعر الخيار بناءً على سعر السهم والوقت؟ على سبيل المثال، يمكننا استخدام شبكة عصبية تغذية أمامية (Feed Forward Neural Network) وتدريبها من خلال الانتشار الخلفي (backpropagation). هذا النهج يمثل أساس استخدام الشبكات العصبية في تسعير الخيارات.

في آلية التدريب هذه، نقوم بتقليل الخطأ:

L = |Estimated C - Real C|:

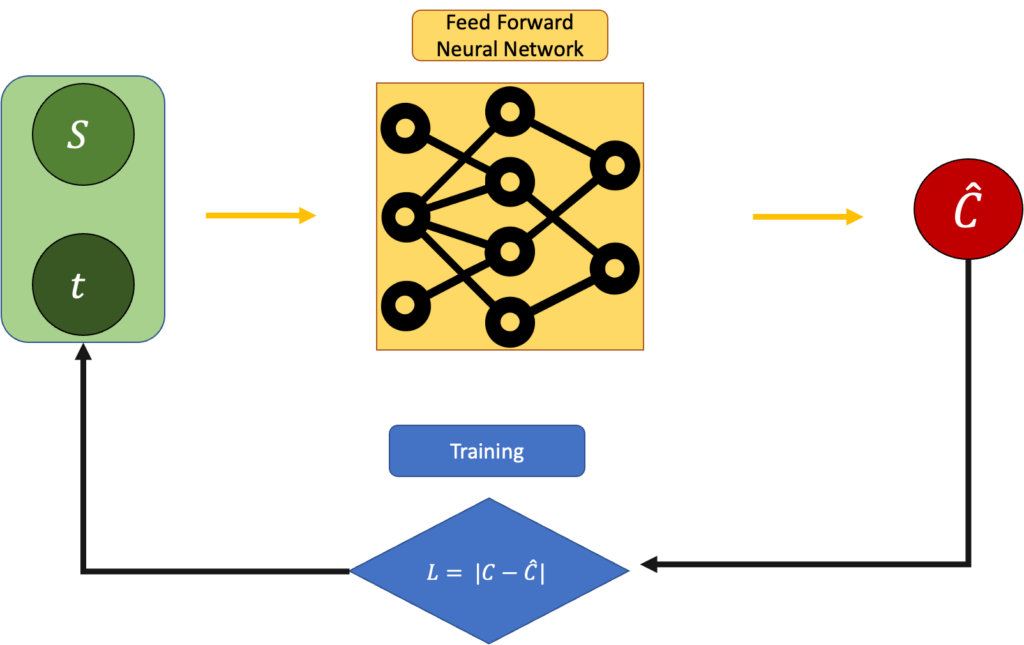
هذا جيد، وهو أبسط نهج للشبكات العصبية يمكنك القيام به. المشكلة هنا هي أننا نتجاهل تمامًا معادلة بلاك-شولز (Black-Scholes equation). إذن، هل هناك طريقة أخرى؟ هل يمكننا دمجها؟

بالطبع، يمكننا ذلك، إذا قمنا بتعيين الخطأ ليكون:

L = |Estimated C - Real C|+ PDE(C,S,t)

حيث PDE(C,S,t) هي:

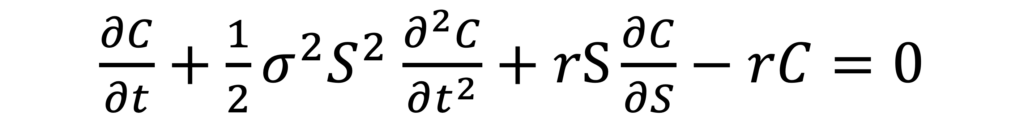
ويجب أن تكون قريبة من 0 قدر الإمكان:

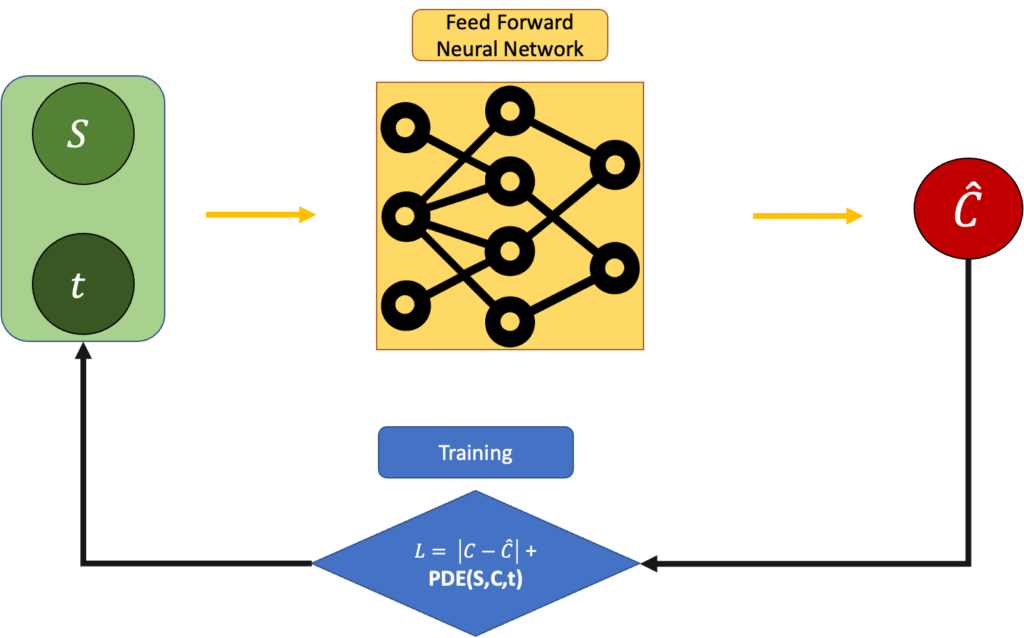
ولكن السؤال لا يزال قائما. لماذا هذا “أفضل” من معادلة بلاك-شولز البسيطة؟ لماذا لا نستخدم فقط المعادلة التفاضلية؟ حسنًا، لأنه في بعض الأحيان، في الحياة، لا يضمن لك حل المعادلة التفاضلية الحل “الحقيقي”. عادةً ما تقوم الفيزياء بتقريب الأشياء، وهي تفعل ذلك بطريقة يمكن أن تخلق فرقًا بين ما نتوقعه وما نراه. لهذا السبب تعتبر الشبكات العصبية المستنيرة بالفيزياء (PINN) أداة مدهشة ورائعة: فأنت تحاول مطابقة الفيزياء، لكنك صارم في حقيقة أن النتائج يجب أن تتطابق مع ما “تراه” من مجموعة البيانات الخاصة بك. هذا التكامل بين النموذج الفيزيائي والبيانات التجريبية هو ما يميز هذا النهج.

في حالتنا، قد يكون الأمر أنه من أجل الحصول على محفظة خالية من المخاطر، نجد أن نموذج بلاك-شولز النظري لا يتطابق تمامًا مع بيانات السوق الصاخبة أو المتحيزة أو غير الكاملة التي نراقبها. ربما التقلب ليس ثابتًا. ربما السوق ليس فعالاً. ربما الافتراضات الكامنة وراء المعادلة لا تصمد. هذا هو المكان الذي يمكن أن يكون فيه نهج مثل PINN مفيدًا. نحن لا نجد حلاً يفي بمعادلة بلاك-شولز فحسب، بل “نثق” أيضًا بما نراه من البيانات. هذا يسمح بنموذج أكثر مرونة وقابلية للتكيف مع ظروف السوق الحقيقية.

حسنًا، يكفي من النظرية. هيا نبرمج. 👨‍💻

3. تطبيق عملي باستخدام Python

يمكنك العثور على الكود الكامل، مع ملف README.md رائع، ودفتر ملاحظات ممتاز، وكود معياري فائق الوضوح هنا. هذا الكود مصمم خصيصًا لحل معادلة بلاك-شولز باستخدام شبكات PINN العصبية، وهو أسلوب متقدم في مجال النمذجة المالية.

ملاحظة: سيكون هذا الجزء مكثفًا بعض الشيء (الكثير من التعليمات البرمجية)، وإذا لم تكن مهتمًا بالبرمجيات، فلا تتردد في الانتقال إلى الفصل التالي. سأعرض النتائج بطريقة أكثر سهولة 🙂

شكرًا جزيلاً لك على وصولك إلى هذه المرحلة ❤️
دعنا نرى كيف يمكننا تنفيذ ذلك. لنستعرض الآن كيفية تطبيق هذه التقنية في حل معادلات بلاك-شولز، مع التركيز على الجوانب العملية والتفصيلية.

3.1 ملف Config.json

يمكن تشغيل الكود بالكامل باستخدام ملف تهيئة بسيط للغاية، أطلقت عليه اسم config.json.

يمكنك وضعه في أي مكان تريده، كما سنرى لاحقًا.

هذا الملف ضروري، لأنه يحدد جميع المعلمات التي تحكم المحاكاة الخاصة بنا، وتوليد البيانات، وتدريب النموذج. دعني أشرح لك بسرعة ما تمثله كل قيمة:

• K: سعر التنفيذ – وهو السعر الذي يمنحك عنده الخيار الحق في شراء السهم في المستقبل.
• T: الوقت حتى تاريخ الاستحقاق، بالسنوات. إذن T = 1.0 يعني أن صلاحية الخيار تنتهي بعد وحدة واحدة (على سبيل المثال، سنة واحدة) من الآن.
• r: معدل الفائدة الخالي من المخاطر المستخدم لخصم القيم المستقبلية. هذا هو معدل الفائدة الذي نحدده في المحاكاة الخاصة بنا.
• sigma: تقلب السهم، والذي يحدد مدى صعوبة التنبؤ بسعر السهم أو مدى “خطورته”. مرة أخرى، هذه معلمة محاكاة.
• N_data: عدد نقاط البيانات الاصطناعية التي نريد إنشاؤها للتدريب. سيحدد هذا أيضًا حجم النموذج.
• min_S و max_S: نطاق أسعار الأسهم الذي نريد أخذ عينات منه عند إنشاء بيانات اصطناعية. الحد الأدنى والحد الأقصى لسعر السهم لدينا.
• bias: إزاحة اختيارية تضاف إلى أسعار الخيارات، لمحاكاة تحول منهجي في البيانات. يتم ذلك لإنشاء تباين بين العالم الحقيقي وبيانات Black-Scholes.
• noise_variance: مقدار الضوضاء المضافة إلى أسعار الخيارات لمحاكاة ضوضاء القياس أو السوق. تتم إضافة هذه المعلمة لنفس السبب كما كان من قبل.
• epochs: عدد التكرارات التي سيتم تدريب النموذج عليها.
• lr: معدل التعلم للمحسن. يتحكم هذا في مدى سرعة تحديث النموذج أثناء التدريب.
• log_interval: عدد المرات (من حيث العصور) التي نريد فيها طباعة السجلات لمراقبة تقدم التدريب.

تلعب كل معلمة من هذه المعلمات دورًا محددًا، حيث يشكل بعضها العالم المالي الذي نحاكيه، بينما يتحكم البعض الآخر في كيفية تفاعل شبكتنا العصبية مع هذا العالم. يمكن أن تؤدي التعديلات الصغيرة هنا إلى سلوك مختلف تمامًا، مما يجعل هذا الملف قويًا وحساسًا. سيؤدي تغيير قيم ملف JSON هذا إلى تغيير جذري في إخراج الكود.

3.2 main.py (ملف main.py)

الآن، دعونا نلقي نظرة على كيفية استخدام بقية التعليمات البرمجية لهذا التكوين عمليًا.

يأتي الجزء الرئيسي من التعليمات البرمجية الخاصة بنا من main.py، لتدريب شبكة PINN الخاصة بك باستخدام Torch، و black_scholes.py.

هذا هو ملف main.py:

إذًا، ما يمكنك فعله هو:

1. إنشاء ملف config.json الخاص بك
2. تشغيل الأمر python main.py --config config.json

يستخدم ملف main.py الكثير من الملفات الأخرى.

3.3 black_scholes.py والمساعدات

يوجد تطبيق نموذج Black-Scholes داخل الملف black_scholes.py:

يمكن استخدام هذا الملف لبناء النموذج وتدريبه وتصديره والتنبؤ به.
تستخدم الدالة بعض الملفات المساعدة أيضًا، مثل data.py و loss.py و model.py.
يوجد نموذج Torch داخل الملف model.py:

يوجد منشئ البيانات (بالنظر إلى ملف التهيئة) داخل الملف data.py:

ودالة الخسارة المدمجة التي تتضمن قيمة الانحراف هي loss.py. هذه الدالة ضرورية لتحسين دقة النموذج.

4. النتائج

حسنًا، عند تشغيل main.py، يتم تدريب شبكتنا العصبية التغذوية الأمامية (FFNN)، ونحصل على ما يلي:

كما تلاحظ، فإن خطأ النموذج ليس تمامًا 0، ولكن معادلة PDE للنموذج أصغر بكثير من البيانات. هذا يعني أن النموذج يقوم (بشكل طبيعي) بفرض تنبؤاتنا بقوة لتلبية المعادلات التفاضلية. هذا بالضبط ما قلناه من قبل: نحن نحسن الأداء من حيث البيانات المتوفرة لدينا ومن حيث نموذج Black-Scholes.

يمكننا أن نلاحظ، نوعيًا، وجود تطابق كبير بين مجموعة البيانات الواقعية المشوشة + المتحيزة (واقعية إلى حد ما) وشبكة PINN.

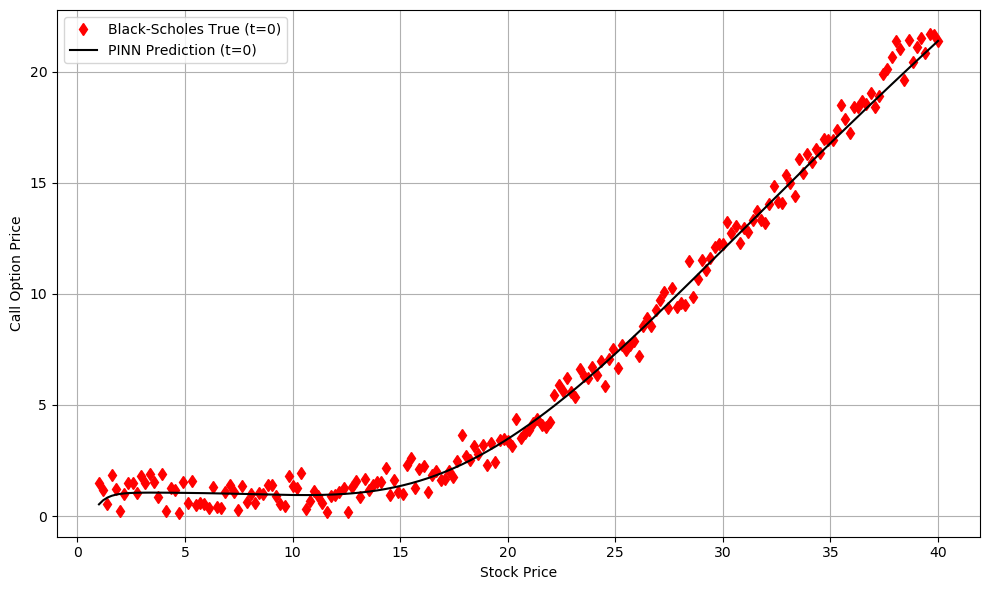
هذه هي النتائج عندما تكون t = 0، ويتغير سعر السهم مع خيار الشراء عند قيمة t ثابتة. رائع جدًا، أليس كذلك؟ ولكن الأمر لم ينته بعد! يمكنك استكشاف النتائج باستخدام الكود أعلاه بطريقتين:

1. اللعب بالعديد من المعلمات (parameters) الموجودة في config.json
2. رؤية التنبؤات عند t>0

استمتع! 🙂

5. استنتاجات

شكراً جزيلاً لوصولكم إلى هنا. حقاً، كانت هذه رحلة طويلة 😅
إليكم ما استعرضناه في هذه المقالة:

1. بدأنا بالفيزياء، وكيف أن قوانينها، المكتوبة كمعادلات تفاضلية، عادلة، وجميلة، وقابلة للتنبؤ (عادةً).
2. انتقلنا إلى التمويل، والتقينا بنموذج بلاك-شولز Black-Scholes Model— وهي معادلة تفاضلية تهدف إلى تسعير الخيارات بطريقة خالية من المخاطر.
3. استكشفنا الشبكات العصبية المستنيرة بالفيزياء (PINNs)، وهي نوع من الشبكات العصبية لا تكتفي بمطابقة البيانات ولكنها تحترم المعادلة التفاضلية الأساسية. تعتبر PINNs أداة قوية في نمذجة الأنظمة المعقدة.
4. نفذنا كل شيء في Python Python، باستخدام PyTorch وقاعدة بيانات معيارية نظيفة تتيح لك تعديل المعلمات، وإنشاء بيانات اصطناعية، وتدريب شبكات PINNs الخاصة بك لحل معادلة بلاك-شولز Black-Scholes.
5. صورنا النتائج ورأينا كيف تعلمت الشبكة أن تطابق ليس فقط البيانات المشوشة ولكن أيضاً السلوك المتوقع من معادلة بلاك-شولز Black-Scholes.

أعلم أن استيعاب كل هذا دفعة واحدة ليس بالأمر السهل. في بعض المجالات، كنت مقتضباً بالضرورة، ربما أقصر مما كنت بحاجة إليه. ومع ذلك، إذا كنت ترغب في رؤية الأمور بطريقة أكثر وضوحاً، مرة أخرى، ألقِ نظرة على مجلد GitHub. حتى إذا لم تكن مهتماً بالبرامج، فهناك ملف README.md واضح ونموذج بسيط example/BlackScholesModel.ipynb يشرح المشروع خطوة بخطوة.